施策を実施した結果、まちがどうなるかは、費用対効果の観点からも大切なことである。地方創生を実践していく中でKPIの必要性が叫ばれ、それとの関連で市町村レベルでの「産業連関表」の作成と利活用が広がってきている。ただ現場感覚としては、それがどの程度実際の施策に生かすことができるのか、作成に対しての費用対効果はあるのだろうか等といった疑問もある。今回と次回の2回で、地域産業連関表の考え方と新たな使い道を解説する。
産業連関表とは
アメリカの経済学者ワシリー・レオンチェフが、1936年にアメリカを対象として作成したものが最初とされ、彼はこの功績で1973年にノーベル経済学賞を受賞している。一般均衡理論を現実の経済に適用しようとしたモデルである。レオンチェフ自身によれば、マルクスの再生産表式から着想したということだが、そのルーツはフランスのケネーの経済表(1758年)にさかのぼる。
ケネーは外科医であったが内科の循環器系にも詳しく、また宮廷においてフランス経済にも関心が強かったことから、経済を内科の血液循環になぞらえて、フランス経済の取引表を作成した。
歴代のノーベル経済学賞の功績の中で最も現実の政策に貢献しているのが、産業連関表(分析)であることは間違いないだろう。そういった意味からも、産業連関表は実物経済の資金循環を見る手立ての1つであると言え、さらに規範的な分析をすることによって様々な地域経済の姿を描写することができるのである。
「産業連関表」の原表記は Input Output Table である。つまり経済活動での「投入と産出の表」のことを意味している。日本語でこれを「産業連関表」と訳したのであるが、産業間のつながりをイメージできる点からも、これは実に名訳である。「産業」は事業所(企業)を産業分類に併せて集計したもので、「連関」は事業所間のつながり(取引額)を産業分類で集計したものである。
「投入・産出」における投入には二つの概念がある。1つは「他から購入する」という仕入れの概念で、原材料、エネルギー、素材、部品等に加えて、保守・点検、輸送、金融、保険のようなサービス、アウトソーシング等も該当する。もう1つは「借りる、所有しているものを使う」という概念で、生産要素としての人、建物や設備、土地等が対応する。
産業連関表の数値は、1年間の取引量の金銭評価額であるので、人については雇用することによって発生する賃金・俸給、購入した建物や設備については、その利用の対価として減価償却費(資本減耗額)、そして土地については借りている場合の地代に相当する金額がそれぞれ対応する。産出(額)とは、活動ベースでとらえた出荷額や販売額の概念であり、どういった経済主体にどれだけ販売されたかというとらえ方をする。なお、産業連関表の数値は、会計上、投入額と産出額(産業連関表での生産額)は一致する。
産業連関表の見方
地域経済を見る上で大事なことは、ものやサービスを、「だれから、どれだけ購入したのか?」に加えて「どこから購入し、どこへ販売したのか?」ということである。一国の場合は、輸出と輸入で表現されるが、地域表の場合は、移出と移入によって表現される。
次頁の図は、非競争移入型の産業連関表である。非競争移入型とは、域外からの移輸入品と域内生産品を区別する、つまり両者を競争的な財としては扱わないものという考え方に依っている。これに対して、移入品も域内品も同じ性質をもつものとして競争的に扱った連関表は「競争移入型」となる。各産業が購入したものは域内品も域外品も合算して中間投入部分に計上し、最終需要のところの移入で一括して控除するという方式である。
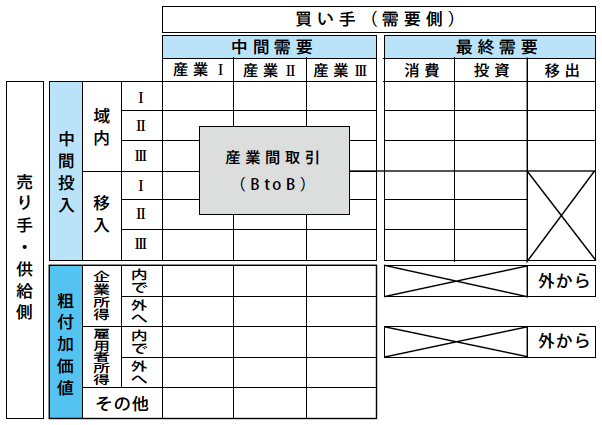
我が国の地域内産業連関表は、多くの政令指定都市や都道府県で作成されているが、そのほとんど全ては競争移入型の表となっている。これは非競争移入型を作成することが、多大な労力を伴うことによっている。一般に、競争移入型の産業連関表は地域経済の予測には適応度が高いが、地域経済の現状分析となると非競争移入型の産業連関表の方が強みを発揮することが知られている。
この図で注目したいのは、粗付加価値部分である。ここにおける企業所得や雇用者所得についても域内外の区別がなされている点である。地域で公共事業を実施することは、受注者が域外の企業であっても発生地であるまちの経済活動として計上される。しかし、企業収入の部分は本社のある他都市に行ってしまう。これは本社サービスの受益とマネーフローの関係から、移入というとらえ方ができる。このことは雇用者所得についても同様である。まちで発生した雇用者所得が、雇用者がまちの外からの通勤者であれば、この所得は域外に漏出する。そして、そこから生じる消費支出もまちの外でなされることになるかもしれない。これら漏出の逆は、移出というとらえ方になる。まちの経済構造を正確に把握するには、こういった型の産業連関表を作成することが意味を持ってくる。
地域の産業連関表から何がわかる?
それでは、こういった産業連関表を作成することによって何が分かるのであろうか。それは大きく2つに分けて示すことができる。
1つ目は、産業連関表をしっかりと読み解いて、「まちの内外」のつきあいがどの様になっているのかを判別できることである。これによって、まちにあるものまで、あるいはまちの企業が供給できるものまで、外から購入している事実が判明することがある。そうすると、どうしてそのようになっているのかを次に考えることになる。もし、「まちの内」で賄うことができれば、それは「まちの外」にお金が出ていくことなく、まちの誰かの所得になるはずである。それならば、そのまち、地域で賄っていない理由は何であろうか?
品質の問題、納期の問題、これまでのつきあい(人間関係)、供給量の問題等が考えられる。こういったことは、政策として対応ができるかも知れない。有効な施策のあり方を考えるいい機会となる。
農産物は食料品製造業で投入要素となり、商業やサービス業でも使われるであろう。工業製品は、個人消費だけでなく、同じ製造業種や農家へも販売されるであろう。金融保険や運輸といったサービスは、農業でも工業でも必要である。そうすると、どの産業でも頑張れば、その効果は、つきあい(取引)のある全ての産業へと波及することになる。
2つ目は、産業連関表は連立方程式になっているので、それを解くことによって、こういった波及効果を定量的に掴むことができるということである。消費や投資、更には移出などの最終需要の変化によって、どの産業がどの程度の影響を受けているのか、また、どこに影響を与えているのかが定量的に分かる。
しかしながら、どの産業も生産したものが売れないと企業が成り立たない。その場合、考え方は2通りある。1つは、消費者(あるいは最終需要者)は必要なものは購入するという前提である。すると需要があるので、そこから派生して生産が生まれるということになる。もう1つは、良いものを作り(商品の差別化)、あるいはこれまでなかったものを作り(技術開発による新製品や新サービス)、消費者の需要を呼び起こすことである。これは、供給が需要を生み出すという考え方である。ガラパゴス系の携帯電話からスマートフォンへの移行がその典型であろう。産業連関分析は、前者の立場をとる。つまり、需要があって供給(生産)が生まれるということである。だから生産波及効果が〇〇万円という表現になる。
市町村産業連関表の意義
生産波及額から生まれる所得に対しての二次波及効果を計算する際に、こういった市町村経済にとって重要なことは、従来ほとんど考慮されてこなかった。
これまでの産業連関表は、国際間のものはあっても地域表は、都道府県、政令指定都市までが主に自治体の手によって作成されてきた。経済規模が大きくない地方の市町村のような小地域の場合、多くが全国GDPの動きでまちの経済が規定されている状況だといって差し支えないであろう。それは地域経済の自立性が低く、地域外からの移入に依存している部分が圧倒的に大きいということを意味している。つまり、わざわざ連関表など作らなくても、全国GDPとの相関さえ見ておけば良いということになるのである。しかしながら、自立を目指すなら、なおのこと「地域の連関構造」がどのようになっているかを、きちんと掴んでおくべきであろう。
小地域の場合は県のような大きな地域と違って、住民との距離が近いところが多い。そういったところでは、きちんとした調査ができる可能性は高く、意義があるといえるであろう。しかも、それぞれの部門での生産活動に用いる原材料や中間財がどこから来ているかを捉えておくことも可能となる。これは、実体経済の分析にパワーを発揮する「非競争移入型」の産業連関表の作成を意味する。
産業連関モデルの前提
産業連関分析を行うときに知っておくべきこととして、いくつかの前提条件がある。産業連関分析は、ある経済構造(1年間の実物経済のマネーフロー)を前提に話を進めることから、いわゆる短期なので生産技術は固定されている。言い換えると、原単位方式であり、資本とは完全補完関係にある。たとえば、ある車1台を生産するのに必要な鉄鋼の投入額は一定比率に保たれている。
産業連関モデルは、最初に需要があって、そこから生産波及効果や所得誘発効果が生まれるというのが基本ロジックである。したがって、基本は下流(最終需要)から上流(企業が生産に用いる中間財生産)への波及効果を見ていることになる。企業の生産活動が活性化するのは、最終需要あってのことなのである。企業が自律的に生産を増やすことは、産業連関表では内生部分(未知数)なのでモデルの想定外だが、その分析も技術的には可能ではある。また、需要が増えても財の価格上昇を伴わず供給(生産)は十分満たされる。そして、最終需要の消費も所与ではあるが、ケインズモデルのように内生化モデルに変えることも可能である。
『ひょうご自治』平成30年1月号に掲載


