1. はじめに
国際貿易の分野では、国際化には高い生産性が必要であると主張する「新々貿易理論」 (firm heterogeneity model) が脚光を浴びている。それに沿う形で、生産性の高い企業ほど国際化する傾向にあるという実証研究も世界各国で出てきている。
他方、国際化企業は外国市場での経験によって非国際化企業よりも高い生産性成長を実現できるとする「国際化による学習仮説」を支持する実証研究も出てきている。今後労働力の増加が期待できない日本において、経済全体の成長には、個々の企業の生産性の向上が求められる。そのため、国際化を通した企業の生産性成長、技術革新は重要な政策課題であり、経済産業研究所 (RIETI) では既にシンポジウム「多様性、国際化、イノベーション:中小企業政策の新しい視点」(注1)を開催している。
こうした中、国際貿易の分野において、企業レベルの生産性の測定に注目が集まっている。RIETIでも、企業の国際化と生産性に関する数多くの研究がなされてきた。そこで、本稿は、生産性について概説するとともに、国際貿易の研究者が実際に生産性をどのように計算しているのかを簡単に紹介したい。
2. 労働生産性
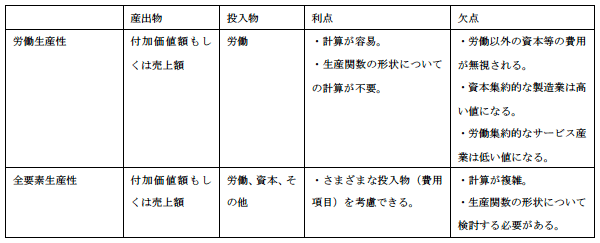
生産性とは、どれだけ少ない投入物でどれだけ多くの産出物を生み出せるかを示すものである。生産性の指標として代表的なものに、(1)労働生産性と(2)全要素生産性 (TFP) がある。
労働生産性は、労働1単位(1人)あたりどれだけの付加価値額(売上額)が生み出されたかを測る指標である(注2)。投入要素は労働のみと仮定するために、計算が非常に簡単である。一方で、コンピュータや機械設備などの資本に要する費用を無視している問題がある。そのため、資本集約的産業の労働生産性は高く評価され、労働集約的産業の労働生産性は低く評価される。たとえば、資本集約的な製造業と労働集約的なサービス産業の生産性を労働生産性で比較すると、サービス産業の生産性が過小に評価されかねない。
3. 全要素生産性(TFP)
それに対して、全要素生産性は、生産に必要なさまざまな投入物を考慮のうえで、それらの投入物によってどれだけの付加価値額(売上額)が生まれたのかを測る指標である(注3)。労働生産性はこの全要素生産性の特殊形と見なすことができる。全要素生産性はよりバランスのとれた生産性指標であるといえる。一方で、全要素生産性を計算するには、労働以外に少なくとも資本のデータが必要になる。資本のデータがないために、現実には全要素生産性を計算できない場合も多い。また、労働や資本といった複数の投入物が付加価値額にどの程度の割合で貢献しているのかを決める必要が生じる。
Head and Ries (2003) が行った近似的全要素生産性 (Approximate TFP) の計算では、対数で評価して、労働が3分の2、資本が3分の1の貢献をすると仮定して、全要素生産性を計算している(注4)。なお、コブダグラス型生産関数のように非線形の生産関数を仮定することが多いため、対数をとることで生産関数を線形にして計算することが多い。近似的全要素生産性には強い仮定(収穫一定等)が必要であり、労働や資本の単位の取り方にも結果が依存する。より精確には労働や資本の貢献の割合を何らかの方法で計算する必要がある。
4. 全要素生産性指標(TFP index)
国際貿易の分野では、全要素生産性の計算に主に2つの手段がとられる。(1)全要素生産性指標の計算と(2)生産関数の推定である。
全要素生産性指標 (TFP index) は、Caves et al. (1982) によって開発され、Good et al. (1997) によって拡張された。国際貿易の分野では、Aw et al. (2000) が用いている。具体的な算出方法はAw et al. (2000) のAppendix Bで詳述されている(注5)。簡単にいうと、各投入要素費用の全費用に占める割合を各投入要素の付加価値額に対する貢献割合と見なす。全要素生産性指標は、その割合で重み付けられた投入要素全体に対してどれほどの付加価値額(売上額)が生まれているのかを測ったものである。全要素生産性指標の計算には、労働費用・資本費用を計算するために賃金や資本レンタル率のデータが必要になる。
5. 生産関数の推定
それに対して、生産関数の推定によって、各投入要素の貢献割合を推定し、全要素生産性を計算する方法もある(注6)。最も単純な方法では、最小自乗法で付加価値額(売上額)を労働や資本に回帰し、労働と資本の推定係数を得る。この推定係数を、各投入要素の貢献割合と見なす。それによって、この推定係数で重み付けされた投入要素全体が、どれほどの付加価値額(売上額)を生んでいるのかを計算することができる。
6. Olley and Pakes (1996) 法による生産関数の推定
ただし、Olley and Pakes (1996) は、最小自乗法による生産関数の推定には計量経済学的に、2つの問題があることを明らかにした。1つは、生産性の高い企業ほど倒産しないので推定に用いる標本に出現しやすいという標本選択問題 (selection problem) がある。
もう1つは、生産性の高い企業ほど投入要素であるはずの資本が多い傾向があるという同時性の問題 (simultaneity problem) がある。
こうした計量経済学的問題を解決するには、まず各企業の生存確率を推定することが必要である。また、分析前には明らかではない各企業の生産性の影響を資本のほかに投資や上記の生存確率を用いて制御する必要がある。それによって、生産性の影響から分離した資本の推定係数を得ることができる。この手法は、Olley and Pakes (1996) によって開発された。ゼロや欠損値が多い投資の代わりに光熱費や原材料費を用いるLevinsohn and Petrin (2003) の方法もある。
7. Olley and Pakes (1996) 法、 Levinsohn and Petrin (2003) 法を実行する配布プログラム
Olley and Pakes (1996) や Levinsohn and Petrin (2003) の手法を用いて生産関数を推定し全要素生産性を計算するのは複雑な作業になる。しかし、Yasar, Raciborski, and Poi (2008) とPetrin, Poi, and Levinsohn (2004) は、これらの手法を統計分析ソフトStataで簡単に実行するためのプログラムopregとlevpetを提供し、解説している。具体的な使用手順は補論に記す。
8. RIETIにおける企業の国際化と生産性に関する研究
RIETIでは、『企業活動基本調査』、『工業統計』、『商工業実態基本調査』等の経済産業省所管の企業レベルデータを用いることができる利点を生かして、生産性と企業の国際化に関する多くの研究が行われてきた。森川(2010)と松浦他(2008)が展望しているように、RIETIでは、国際貿易に限らず、幅広く生産性の研究が行われているが、本稿は国際貿易の分野での生産性に関する研究を簡単に紹介する。
多くの研究の中でも、若杉他 (2008) と八代・平野 (2010) は、それぞれOlley and Pakes (1996) 法、Levinsohn and Petrin (2003) 法を用いて測定した全要素生産性と企業の国際化との関係を分析している。国際化開始企業の方が国際化非開始企業よりも生産性成長が高いことを明らかにした若杉他 (2008) の研究成果は2010年度の『通商白書』にも転載されている。冨浦英一RIETIファカルティフェロー/横浜国立大学教授の研究は、近似的全要素生産性を用いて、世界に先駆けて企業の生産性と外国生産委託との関係を分析している(Tomiura (2007) )。
表2は、生産性と企業の国際化に関する代表的な既存研究をまとめたものである。

9. 終わりに
本稿では、国際貿易の分野でよく用いられている手法に絞って、簡単に生産性とその計算方法を紹介してきた。Van Biesebroeck (2007) はより広範かつ詳細に生産性の計算方法の紹介と比較を行っている。
謝辞
伊藤萬里・専修大学講師兼RIETI研究員、松浦寿幸・慶應義塾大学講師をはじめとする先生方の日頃の御教示に本稿の内容は多くを負っている。


