企業間の依存関係がある下での生産関数の推定方法

政策評価プログラム（第五期：2020〜2023年度）
「総合的EBPM研究」プロジェクト

本稿では、地域内の企業間での依存関係がある下での企業の生産性を推定するため、3段階の一般化モーメント法（GMM）推定法を提唱している。同手法は、Ackerberg, Caves, and Frazer (2015)とWooldridge (2009)の既存の手法に基づきながら、企業の生産性が地域内の企業の生産量、投入量、共通するショックに依存することを許している。これは例えば、地域内の同産業他企業の生産投入量（例、労働など）が増えれば、集積の経済により自企業の生産性に影響を与えるケースや、取引企業間での知識の波及が企業の生産性に影響を与えるケースなどを考慮している。

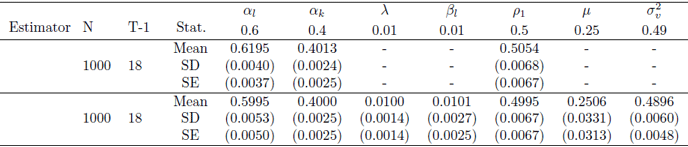
推定手法の精度を確かめるためにモンテカルロ・シミュレーションを用いた結果、提唱している推定法は企業間の依存関係が有る無しにかかわらず、生産関数や生産性の依存関係に関するパラメータの一致推定量（分析の観測数が大きくなれば、推定したパラメータの値が真の値に近くなる）を導く一方（表1、表2下）、既存の生産関数の推定法を用いると、企業間の依存関係が有る場合には推定値にバイアスが生じることが分かった（表2上）。

そして本研究では、構築された手法を、企業間取引ネットワークをカバーしている日本の企業レベルパネルデータに応用した。その結果、企業の生産性が、地域内の企業の生産量、投入量、共通するショックに依存していることを発見した。

注：\(α_l\)と\(α_k\)は、それぞれ生産関数の労働と資本の係数。\(λ\)と\(β_l\)は、それぞれ企業の生産性が他企業の生産量と投入量に依存する程度を表す係数。\(ρ_1\)は今期と前期の生産性の依存程度を表す係数。\(μ\)は企業の生産性の誤差項が他企業の誤差項に依存する程度を表す係数。\(σ_v^2\)は企業の生産性の誤差項の分散を表す係数。NとTは、シミュレーションにおける企業数と年数。表2行目は、シミュレーションで仮定したそれぞれのパラメータの真の値を示している。Mean、SD、SEは、シミュレーションを500回行って得られた推定里の平均、標準偏差、標準誤差を表す。

注：表1と同じ。