| 執筆者 | 矢野 誠 (所長,CRO)/古川 雄一 (ファカルティフェロー) |
|---|---|
| 研究プロジェクト | 市場の質の法と経済学に関するエビデンスベースポリシー研究 |
| ダウンロード/関連リンク |
このノンテクニカルサマリーは、分析結果を踏まえつつ、政策的含意を中心に大胆に記述したもので、DP・PDPの一部分ではありません。分析内容の詳細はDP・PDP本文をお読みください。また、ここに述べられている見解は執筆者個人の責任で発表するものであり、所属する組織および(独)経済産業研究所としての見解を示すものではありません。
法と経済プログラム(第四期:2016〜2019年度)
「市場の質の法と経済学に関するエビデンスベースポリシー研究」プロジェクト
「いずれ、自己を複製し改善することができるAI (人工知能) が開発されるだろう。」
このような見方は、現代においては広く共有されている。しかし、 半世紀以上前にすでに、20世紀を代表するアメリカの数学者であり、現代コンピューターの父とも呼ばれるジョン・フォン=ノイマン (1903-1957) は自己増殖型オートマトンの開発に着手していた (von Neumann 1966)。現代経済はAIとビッグデータが主導する「第4次産業革命」をまさに経験しているところであり (『通商白書2017』第3部第4章)、このような 自己増殖的AI の登場は、いよいよ現実味を帯びてきたといってよい。事実、最新のニュースによれば、そのような機械をつくる方法を明らかにしたニューラルネットワークに関する研究論文が、昨年、既に発表されている (Chang and Lipson 2018)。
アメリカ数学会によるフォン・ノイマンへの追悼特集において、Ulam (1958, p. 5) は次のようなノイマンの発言を回想している (著者による意訳である)。
継続的に進歩する技術とそれによる人間の生活様式に起こるさまざまな変化を見ていると、いったん越してしまうと私たちがよく見知っているような普通の人間生活が継続できなくなってしまうような、人類の歴史上における、ある本質的な特異点(シンギュラリティ)に近づいているように見える。
自己増殖的AIの登場がいよいよ現実的になってきた昨今において、1つの重要な新課題は、このノイマンがいうシンギュラリティとは、具体的に、いったいどのような状態なのだろうか、を問うことであろう。本研究は、市場に摩擦が存在しない完全競争の仮定の下、このような自己増殖的AIに関する問いに経済学的に答える最初の試みである(注1)。
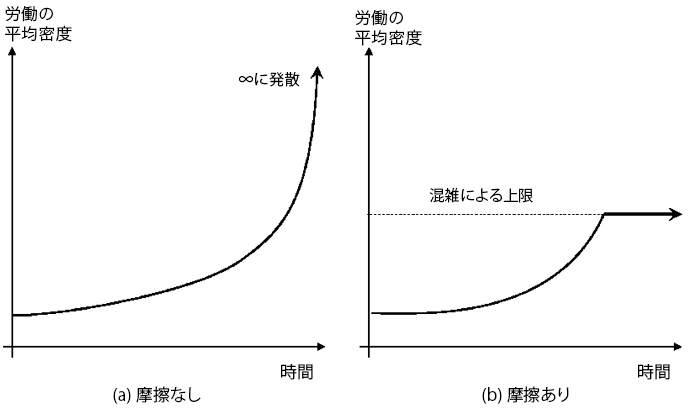
(完全雇用均衡を想定)
本研究の最初の結果は、もし市場だけでなく生産技術にも摩擦がなければ、自己増殖的AIの存在によって、すべての労働者は、最終的には、 (AI と比べて) もっとも人間向きの仕事がある生産セクターに吸収される。 図1(a) は、この状況における、各セクターの平均的な労働密度 (総雇用者数/人間労働を雇用するセクター数) の時間経路をしめしている。時間とともに平均労働密度は発散していく様子が描かれている。つまり、人間労働が、最も人間向きの職場 (生産セクター)に吸収されていく過程において、労働の平均密度は無限大に発散している、本研究は、このすべての人間労働が吸収されていく、 最も人間向きの生産セクターを経済ブラックホールと名付けた。
この分析結果が示していることは、摩擦がまったく存在しないような高質な市場が存在するならば、ひとつの自然現象として、このような経済ブラックホールとなるセクターの現出は避けられないということである。ここでいう摩擦がまったく存在しない状況とは、価格が完全伸縮的であるだけではなく (摩擦のない市場)、生産技術が規模に関して収穫一定 (一次同次性) であるため、どれだけ大量の労働者が1つのセクターに集中しても生産性が低下しないことをも意味している (摩擦のない技術)。この伸縮的価格と生産技術の一次同次性という性質は、新古典派モデルを構成する本質的な仮定でもある。したがって、新古典派的世界においては、自己増殖的AIによる経済ブラックホールの生成は必然であるといえる。
これまでに、多くの人々によって、AIが人類にもたらす帰結に関する懸念が表明されているが、そこでの中心問題は、しかし、われわれの示すような経済ブラックホールではなく、人間の仕事がAIによってとって代わられて、全労働者が失業してしまうのではないか、という可能性である(注2)。
本研究の分析から言えるのは、このような「AIがもたらす失業」を発生させる摩擦要因は、少なくとも、市場か生産技術のどちらかに関係するということである。本研究は、自己増殖的AIを分析する最初の研究として、摩擦のない市場を想定している。なので、生産技術の方に摩擦を導入することで、AIと失業の関係を見ることにする。
シンプルな方法として、人間労働による生産活動には、混雑による雇用規模の上限が存在すると仮定する。この時、均衡において、すべての労働者が最終的にはAIにとってかわられて、経済は完全な失業という状態に陥る可能性があることを、本研究は示した。図1(b) は、このケースにおける平均労働密度の時間経路を示している。生産に摩擦があれば、労働密度は発散せず、上限にとどまり続ける。この背後で、人間を雇用するセクターの数は減少していくので、人間労働の総雇用数 (=雇用セクター×平均労働密度) は単調に減少していき、有限期間のうちに労働需要ゼロ、雇用ゼロの状態に向かっていく。この現象を、われわれは労働シンギュラリティと名付けた(注3)。
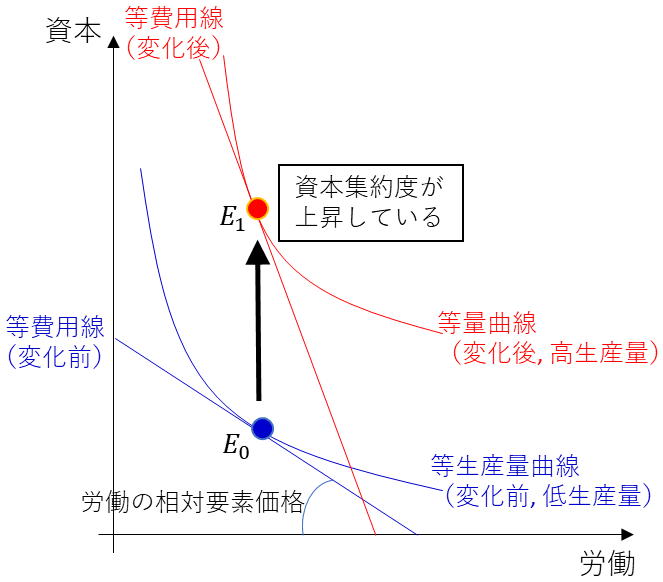
長い歴史の中で、人類は数多くの技術を発明してきた。革新的な技術が開発されるたびに、労働者はそれまで働いていた労働集約的な生産セクターから、新技術が新たに創出した資本集約的な生産セクターへと移行してきた。この労働の移行プロセスは、基礎レベルの経済学で用いられる、資本と労働の等量曲線によって説明することができる。労働供給量が一定のまま、資本が増加したとすれば、何が起こるか。図2に描かれているように、価格効果を通じて相対賃金は上昇し (青色の等費用線から赤色へシフト)、変化前の均衡 (E0) と比べて、変化後の均衡 (E1) ではより資本集約的な生産活動が行われることになる。
歴史的には、資本増加は非常にゆっくりとしたスピードで、かつ、めちゃくちゃにその時代その時代において、ある程度の上限をともなって発生してきた。しかし、自己増殖的AIが登場すれば、ノイマンのシンギュラリティへの言及に象徴されるように、状況は一変するものと予想されている。上の教科書的説明では、自己増殖的AI後の世界を正確に描くことはできない。本研究は、ノイマンのシンギュラリティを経済学的に記述し、より深い理解を得るために、自己増殖的AIの自律成長プロセスを摩擦のない新古典派経済モデルに導入した。結果として示された経済ブラックホールと労働シンギュラリティは、ノイマンのシンギュラリティが含む可能性の一部であるだろう。
われわれの分析結果を考察することで、経済ブラックホールと労働シンギュラリティを避けるにはどうしたらよいか、という問いに関して、重要な示唆を得ることができる。簡単にいえば、労働生産性の成長率が、自己増殖的AIの成長率とバランスしうる経済構造があれば、これらを回避することができる。そしてこれを実現するための答えは、自己増殖的AIそのものにあるかもしれない。なぜなら、AIの拡大は、 一方で、経済ブラックホールや労働シンギュラリティによって人間労働をある意味において阻害する力があるが、他方で、総アウトプットを安定的に上昇させていくからである。もし豊富な生産物を、資源として、教育投資やイノベーション投資にうまくつなげることができたら、労働生産性の成長スピードを自己増殖的AIに匹敵するくらい高めることができるかもしれない。
- 脚注
- 参考文献
-
- 経済産業省, 2017. 『通商白書2017』.
- Acemoglu, D., and P. Restrepo, 2018. "The race between man and machine: Implications of technology for growth, factor shares and employment." American Economic Review, 108, 1488-1542.
- Aghion, P., B. F. Jones, and C. Jones, 2019. "Artificial intelligence and economic growth." in The Economics of Artificial Intelligence: An Agenda, Agrawal, A., J. Gans, and A. Goldfarb, eds., 237-282. University of Chicago Press.
- Boldrin, M., and D. K. Levine, 2002. "Factor saving innovation." Journal of Economic Theory 105, 18-41.
- Chang, O., and H. Lipson, 2018, "Neural network quine," arXiv:1803.05859v4 [cs.AI] 24 May 2018.
- Medeiros, J., 2017. "Stephen Hawking: `I fear AI may replace humans altogether,' WIRED, 28 Nov. 2017.
- Ulam, Stanislaw, 1958. "Tribute to John von Neumann," Bulletin of the American Mathematical Society, 64-3, part 2.
- von Neumann, J. 1966. Theory of Self-Reproducing Automata, University of Illinois Press, Urbana and London.
- Zeira, J., 1998. "Workers, machines, and economic growth." Quarterly Journal of Economics, 113, 1091-1117.

