| 執筆者 | 猪瀬 淳也 (東京大学) |
|---|---|
| 研究プロジェクト | 持続的成長とマクロ経済政策 |
| ダウンロード/関連リンク |
このノンテクニカルサマリーは、分析結果を踏まえつつ、政策的含意を中心に大胆に記述したもので、DP・PDPの一部分ではありません。分析内容の詳細はDP・PDP本文をお読みください。また、ここに述べられている見解は執筆者個人の責任で発表するものであり、所属する組織および(独)経済産業研究所としての見解を示すものではありません。
新しい産業政策プログラム (第三期:2011〜2015年度)
「持続的成長とマクロ経済政策」プロジェクト
CES型効用関数はマクロ経済学などで頻繁に用いられる関数形であるものの、生産関数とは異なりそのミクロ的基礎付けが十分検討されているものではない。本稿は、CES型効用関数のミクロ経済学的基礎付けを検討し、代替の弾力性などに対しても新たな解釈を提供することを目的とした。ミクロ経済学的基礎付けを考慮するにあたっては、本稿では離散選択(Discrete Choice)および分離可能性(Separability)の双方が存在する経済を仮定した。
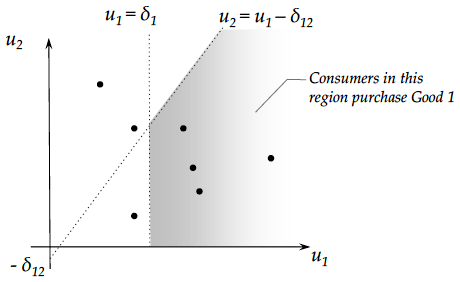
具体的には、多様な消費者のもとで、1つの離散選択の財群および1つの複合材(Composite Goods)からなる経済を考え、モデル化を試みた。この前提のもとで、多様な消費者が離散財(Discrete Goods)に感じる効用に関する分布の関数形を仮定することなどにより、CES型効用関数を導出した。
本稿で採用した仮定に基づけば、根幹的な仮定の1つである各々の離散財への信頼性が変わったとしても、CES型効用関数の代替の弾力性は不変だが、\(X_i^σ\)の係数が変化することとなる。
上述する分析フレームは、高付加価値化などによる差別化ができている産業/できていない産業の選り分けに貢献することができる。今後我が国が成長を持続させていく上でイノベーションを活性化し、より効率的に高付加価値化を図るためにも、国内で強化すべき産業を定量的に評価していくことは肝要であり、政策的意義も大きいものと考えられる。