| 執筆者 |
Adrien BLANCHET (Université de Toulouse) Pascal MOSSAY (University of Reading and CORE) Filippo SANTAMBROGIO (Université Paris Sud) |
|---|---|
| 研究プロジェクト | 都市の成長と空間構造に関する理論と実証 |
| ダウンロード/関連リンク |
このノンテクニカルサマリーは、分析結果を踏まえつつ、政策的含意を中心に大胆に記述したもので、DP・PDPの一部分ではありません。分析内容の詳細はDP・PDP本文をお読みください。また、ここに述べられている見解は執筆者個人の責任で発表するものであり、所属する組織および(独)経済産業研究所としての見解を示すものではありません。
地域経済プログラム (第三期:2011~2015年度)
「都市の成長と空間構造に関する理論と実証」プロジェクト
都心部への家計および企業の集積を取り上げる研究は多くなされている。先行文献の大半が、市場のメカニズムを介する集積要因に研究の焦点を置いている。たとえば、NEG(New Economic Geography:新経済地理学)のモデルは、経済活動の空間的集中を説明するのに、規模に関する収穫逓増の重要性を強調している。
本稿では、都市への個人の集積に寄与する、非市場要因の役割を取り上げている。特に、個人同士の社会的相互作用が、都心センターの分布をどのように形成し得るかを分析した。本稿のモデルは、Beckmann(1976)が構築し、その後Fujita and Thisse(2002)、更に最近ではMossay and Picard(2011)が再考を加えた枠組みを基に構築した。これら先行文献においては、土地利用に関して極めて特定の選好を有する主体者で形成される一次元の経済を仮定して、都市内の分布を求めている。
本稿では、モデルの定性的性質が、より一般的な環境においても成り立つか否かを調べている。そのため、土地消費に関する個人の選好をより一般的な関数にし、空間経済を二次元に拡張して分析を行った。本稿では、均衡が成立するための空間経済の条件と、当該均衡が一意であるための条件を得た。
分析結果を図によって理解してもらうために、二次元空間経済、沿岸都市、都市アメニティを含むいくつかの例を提示する。
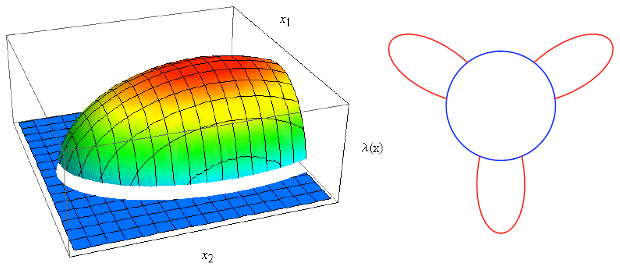
本稿では、Beckmannの枠組みを、土地に関して増加凹関数の効用を持つ個人で形成される二次元空間経済のケースへの一般化を試みた。興味深いことに、空間的均衡をある関数の最小解として導き出せることが明らかになった。そうした最小解は一般に、分析が容易であり、空間均衡の特定も容易なため、有用な結果であるといえる。本稿のモデルでは、複数の均衡の出現は、凸性の欠如によるものであった。線分に沿って出現する集積は1つであるが、円周経済に沿って出現する集積は複数である。本稿での複数均衡が生じる理由は、市場を介する集積要因が原動力となるFujita and Ogawa(1982)の都市モデルのそれとは異なる。
我々の分析結果から、以下の政策的含意を導き出すことができる。1つ目は、空間集積の出現と内部分布を説明する要因として、市場要因に加えて非市場要因と都市アメニティを考慮すべきであるという点である。2つ目は、唯一の都市パターンが生じる条件を分離することで、空間経済における複数均衡の一般的な性質が明らかにした点である。したがって、こうした観点から、ある均衡から別の均衡への移行が可能であるため、都市パターンの変遷は歴史の影響を受ける。さらに、政策立案者らは、望ましい均衡へ誘導するための政策を行うことに関心を持つと考えられる。

