| 執筆者 | 成田 悠輔 (客員研究員)/矢田 紘平 (イェール大学) |
|---|---|
| ダウンロード/関連リンク |
このノンテクニカルサマリーは、分析結果を踏まえつつ、政策的含意を中心に大胆に記述したもので、DP・PDPの一部分ではありません。分析内容の詳細はDP・PDP本文をお読みください。また、ここに述べられている見解は執筆者個人の責任で発表するものであり、所属する組織および(独)経済産業研究所としての見解を示すものではありません。
その他特別な研究成果(所属プロジェクトなし)
アルゴリズムを利用した意思決定が爆増している。たとえば機械学習アルゴリズム。機械学習(「人工知能」)による予測や分類を用いた意思決定が雨後の筍状態である。Amazon、Facebook、Google、Microsoft、Netflixをはじめとするウェブ企業は、表示するコンテンツ(映画、音楽、ニュース等)や広告の選択、価格や検索結果順位の決定といった問題に、機械学習を応用している。また、UberやLyft、DiDiといった自動車共有サービスの価格は、各時点・場所における需要と供給の情報をもとに、独自のアルゴリズムによって決定されている。
機械学習アルゴリズムを利用した意思決定は、デジタル世界以外でも爆増している。例えば裁判や保釈判決がその例だ。米国企業Northpointe(現Equivant)が開発したソフトウェアCOMPASは、教師あり機械学習を用いて被告人の再犯確率を予測する。COMPASの予測した危険指数は、米国の多くの裁判官の判断材料として実際に利用されている。その他、機械学習アルゴリズムを用いた人事採用システムも登場している。表1にこれらの例の一部をまとめた。
| アルゴリズムが用いる変数(X) | アルゴリズムの意思決定(Z) | 結果変数(Y) | アルゴリズム例 | |
|---|---|---|---|---|
| ウェブ企業 | 利用者の属性や行動履歴、アクセスの時間・場所 | 表示コンテンツ | 利用者がコンテンツにアクセスしたかどうか | バンディットや強化学習 |
| 自動車共有サービス | 利用者がアプリを開いた時点における周辺地域の需要と供給の情報 | サービスの価格 | 利用者がサービスを利用したかどうか | 価格上昇(動的価格決定) |
| 裁判官 | 被告人の犯罪歴や属性 | 釈放すべきか否か | 被告人が再犯したかどうか | 教師あり学習 |
機械学習以外のアルゴリズムも枚挙にいとまがない。例えば、世界各地の学校選択・入試制度や労働市場・臓器移植市場などでは割当アルゴリズムが用いられている。国債市場や卸売市場からオンラインの広告や中古品市場まで、オークションアルゴリズムが用いられる場面も数多い。その他多くの公共政策領域でも、アルゴリズム的ルールを用いて誰が政策の受益者になれるかが決まる場面は多い。コロナ対策の雇用調整助成金や持続化給付金がその例だ。このような市場制度設計や受益資格決定もまたアルゴリズムを用いた意思決定である(表2)。
| アルゴリズムが用いる変数(X) | アルゴリズムの意思決定(Z) | 結果変数(Y) | アルゴリズム例 | |
|---|---|---|---|---|
| 学校選択制・中央集権入試 | 家庭の学校への選好、学校での優先権 | 学校への割り当て・入学権 | 将来の成績や収入など | 受入保留アルゴリズムなどの割当アルゴリズム |
| オークション | 入札者の入札額 | 入札者が落札したか | 入札者の将来の経済パフォーマンス | オークション・アルゴリズム |
| 雇用調整助成金や持続化給付金などの資格判断 | 家庭や企業の経済状態や規模・構成 | 受益資格があるかどうか | 将来の経済・健康状態 | 受益資格決定規則 |
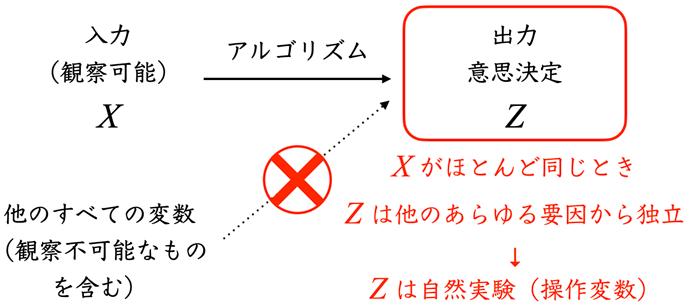
アルゴリズムによる意思決定はすべて面白い共通点を持つ。意思決定の出力が観察可能な入力変数のみに基づくため、入力変数に条件付ければ意思決定があたかも実験のようにランダムに行われるという性質だ(図1)。つまり、アルゴリズムは自然実験であり、操作変数である。例えば、多くの確率的な強化学習・バンディットアルゴリズムは選択(探索)をランダムに行うため、ほとんどランダム化実験(RCT)そのものである。
また、教師付き学習で予測された何らかの変数がある基準値を上回るかどうかで選択を決めるアルゴリズムを考える。この場合、基準値の近くでは、ほぼ同じ状況であるにも関わらず、基準値をたまたま上回ったかどうかというほとんど偶然の要因で異なった意思決定が行われる。これも局所的な自然実験とみなせる。
私たちは、この観察を一般のアルゴリズムについて定式化し、アルゴリズムが自然に生成したデータから因果効果を推定する手法を提案する。主定理として、提案する推定量が一致性と漸近正規性を持つことを示す。この結果の特殊ケースとして、回帰不連続デザインの高次元版も開発する。私たちの推定量は、高次元回帰不連続デザインにおいて一致性・漸近正規性が示されたおそらく唯一の推定量である。提案手法は、PythonやRのパッケージで実装可能である。
証明はこれまで因果推論・経済学では用いられたことのない微分幾何学と幾何学的測度論の手法に基づく。これらの数学的手法は他の問題にも応用が効くかもしれない。
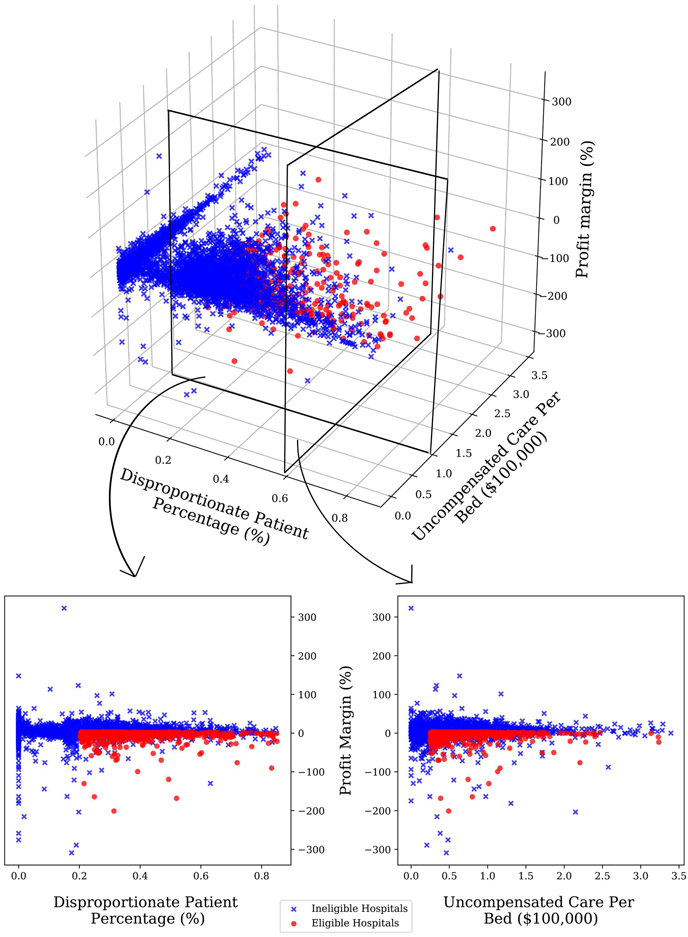
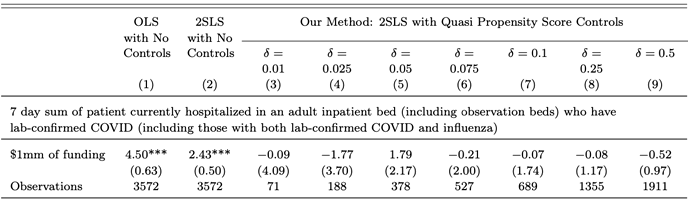
この手法が使える場面は、ビジネスから政策まで幅広い。具体的な実政策応用として、米国の新型コロナウイルス感染症対策の一環として病院への巨額の支援が行われたCARES Act(コロナウイルス支援・救済・経済安全保障法)の効果を分析した。この制度では、支援金の受給資格がアルゴリズム的ルールで決まるため、提案手法を応用できる(図2)。表3は、提案手法による分析の結果(3—9列目)と、受給資格ルールが生み出す自然実験を使わない素朴手法による結果(1・2列目)を比較したものだ。素朴手法では支援金に有意な効果があるように見える。だが、私たちの提案手法による分析の結果、支援金は「コロナ患者のための病床使用数」といった病院のコロナ関係の活動水準にほとんど影響を与えなかったことが分かった。
最後に、同じ技術を用いて様々な政策・ビジネスアルゴリズムの改善も行えるという未来展望を与える。今はウェブ産業に集中しているデータとアルゴリズムの価値をより広い社会に還流するために、私たちの提案技術が役立つことを祈っている。