概要
ミンサー方程式*は、おそらく実証研究で最も広く使用されている方程式であり、経済的現象のみならず、非経済的現象の説明にも利用できる。その一例として、就業収入を学歴や労働市場での経験の関数として説明(および推定)することが挙げられる。ミンサー方程式で教育を1年追加した場合の平均的な金銭的リターンが推定でき、これは教育支出や、教育レベルの優先順位付け、学生ローンなどの教育資金プログラムに関する政策決定を行う政策立案者にとって、非常に重要な情報となる。
主な研究結果
プラス面
- ミンサー方程式を用いることにより、学歴と労働市場における経験で就業収入を説明することができる
- ミンサー方程式の結果は比較が容易なため、どの程度教育に投資すべきか、個人の判断材料としてこれらの結果を活用できる
- ミンサー方程式を用いた最近の研究では、現在は初等教育よりも大学教育(高等教育)が最も高いリターンをもたらす可能性が示唆されており、これは従来の常識からの変化を表している
マイナス面
- 学歴と収入の関係は、必ずしも因果関係を意味しない
- 収入関数は、教育の私的(つまり個人の)収益率を示すものであり、社会的収益率の推定には、教育にかかる政府・公共支出や賃金以外の便益も特定する必要がある
- 経済が複雑化し、技術の進展によって教育への需要が変化する中、数十年前の横断的データが現在の投資判断におけるリターンの指標として有益とは限らない
著者からのメッセージ
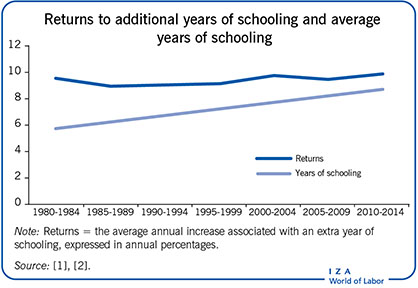
ミンサー方程式によると、教育を1年追加した場合の学校教育の私的(つまり個人の)収益率は8~10%程度となり、国によっては低い場合で0.2%、高い場合は35%以上になることもある。世界平均で、大学教育(高等教育)のリターン(14.5%)が最も高く、次に初等教育(10.2%)、そして中等教育が続く。この結果は、従来の研究結果からの大きな転換を示しており、政策立案者にとっては得るところが多い。たとえば、大学教育のさらなる拡充は個人に極めて有益であると考えられ、政府はより簡便な教育資金の調達手段を模索するべきである。また、女子教育への投資も高いリターンを見込める。
*RIETI 編集部補足:
ミンサー方程式(Mincer earnings function)は、労働経済学の父と呼ばれるJacob Mincerによって提唱されたモデル。
本稿は、2024年8月にIZA World of Laborにて掲載されたものを、IZAの許可を得て、翻訳、転載したものです。


