新型コロナウイルス感染症(以下では「新型感染症」)について1カ月前にコラムを書いたときに、不思議に思ったことがあった。時点ごとの感染者数が正規分布の曲線になっていたことだ[1]。厚生労働省と専門家会議が示した「新型コロナウイルス対策の目的」という資料でも時点ごとの患者数が正規分布の曲線になっている。どうして一定のピークを経て感染者数(患者数)が減少に向かうのかがよく分からなかった。
最近になって、SIRモデルという感染症のモデルを知った。とても興味深いので、私の理解を書き留めておくことにした。私は専門家ではないので、以下の話は批判的に読んでいただき、できれば専門家がもっと緻密で国民に分かりやすい解説をしていただくことを期待している。
SIRモデル
SIRモデルでは、ある感染症について、S(susceptible)が感染症への免疫がない人々、I(infected)が感染症に現在かかっている人々、R(recovered)が感染症から回復して感染症への免疫が生じた人々を指す。以下では数式を使っているが、私は文系の高校数学の知識しかなく、しかも微分積分はもう覚えていないので、加減乗除しか行っていない。従って難しくない。
第t週(ここでは週ごとにした)におけるS、I、Rの人数をそれぞれS(t)、I(t)、R(t)とする。(1)式は感染症への免疫がない人のt週からt+1週への増減を示す。ここではいったん感染したら免疫ができて感染しなくなると仮定されているので、Sの値は減少するだけだ。右辺はこの1週間の新しい感染者数を示している。全ての人々が免疫がないと1人の感染者がうつすのはb人だが、だんだん免疫ができる人々が増えてくるので、t時点では、誰も感染していなかった時の人数であるS(0)に対するS(t)の割合だけうつすことになる。例えば、S(0)が1億人の時に、感染者が増えたためにS(t)が5000万人になると、S(t)/S(0)=0.5となって、うつす相手は当初の半分になる。t時点において他人にうつす能力があるのはその時点の感染者数のI(t)なので、それをかけて、(1)式になる。
S(t+1) - S(t) = -b × S(t)/S(0) × I(t)・・・(1)
次に、(2)式はt週からt+1週にかけて感染から回復した人々の数を示す。ここでは回復した人々は免疫ができた人々と同じであって、Rの値は増加するだけになる。1週間毎に感染症から回復する割合がcとする。cが1/2でI(t)が1000人だとすると、1週間後に500人が回復することになる。
R(t+1) - R(t) = I(t) × c・・・(2)
(3)式はt週からt+1週への感染者数の増減を示す。(1)の感染者数の増加分から(2)の回復者数をひいたものになる。
I(t+1) - I(t) = b × S(t)/S(0) - I(t) × c・・・(3)
S(0)、I(0)、R(0)はそれぞれ1億人、0人、0人で、S(1)、I(1)、R(1)は9999万9999人、1人、0人とする。100週目であるt=100までエクセルで計算してみた。式は図1のようになる。

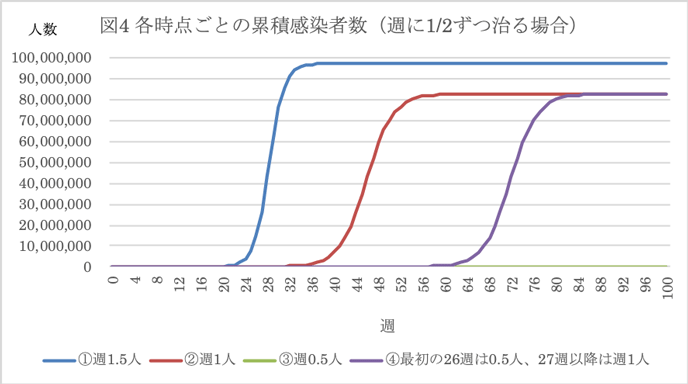
図2にb=1.5、c=1/2の場合の結果が示されている。正規分布に近い曲線が出来上がった。この場合、感染者は週に1.5人ずつ感染症を他人にうつして、2週間たったら治って、もううつさなくなるし、免疫ができてかからなくなる。ピークは28週目で、約3671万人の感染者数がいて、58週時点で感染者は1人より少なくなる。ほとんどの人々が感染して免疫ができたために、感染が止まったことになる。
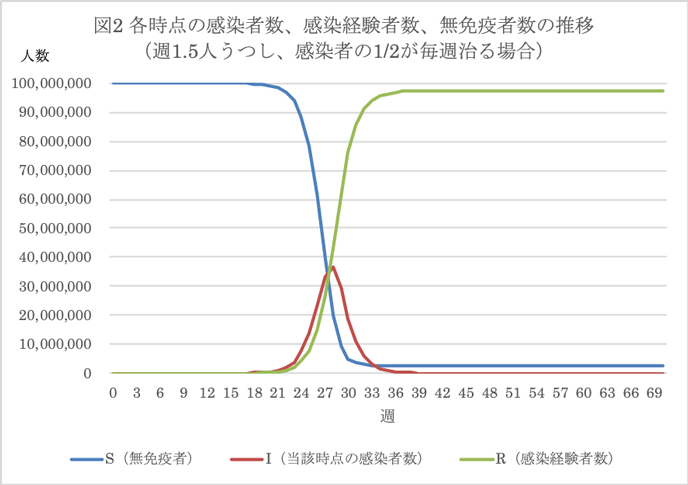
今度は、4つのパターンに分けて、当該時点の感染者数と累積の感染経験者数を見ることにした。4つのパターンとは、上と同じの①週1.5人にうつす、②週1人にうつす、③週0.5人にうつす、④26週までは週0.5人にうつして、27週目から週1人にうつすというものである。 図3に示すように、①に比べて②では感染ピークが低く、ピーク時期も遅くなっており、さらに③では感染スピードがとても遅くなって、各時点の感染者数がこの図ではほとんどわからないぐらい少なく、ピークもこの時間軸では見えない。一方で、④では②に比べてピークが後ろにずれただけでピークの高さは②に近い。
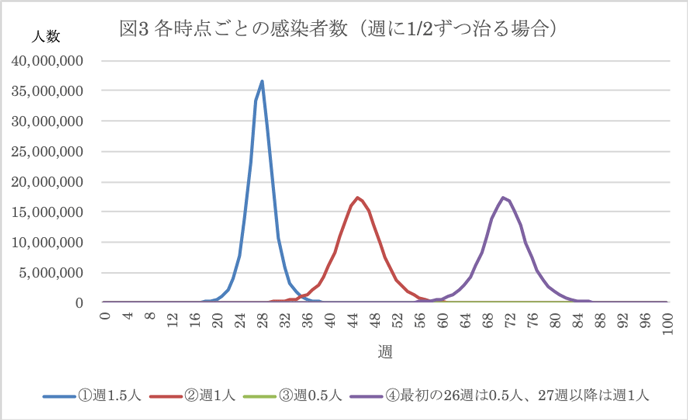
次に、各時点の累積の感染経験者数が図4に出ている。④は②に比べて最終的にはあまり違いがないが、後ろ倒ししたことになる。100週目時点で①より②は約1470万人少なくなっている。③は100週時点の累積の感染経験者数がおおむね50万人となっている。
まとめると、①の週に1.5名ずつうつすパターンが特段の対応策をとらない場合として、②の1/3の削減ではピークを後ろ倒しにしてピークの高さを減らし、最終的な感染者数を9751万人から8281万人に減らす。③の2/3の削減では各時点の感染者数が少ないまま推移して、目に見えたピークは100週までには至らない。ところが、④のように半年間頑張って2/3削減してもその後は1/3の削減(②と同じパターン)に戻すと感染を後ろ倒しにするが、結局は感染者数はあまり変わらない。
感染症の正規分布的な曲線が出来上がるのは、感染症にかかる人々が増えるにつれてもうかからない人々(免疫ができる人)が増えていって、うつす人が少なくなるためであるようだ。また、④にあるとおり、強力な対策で感染者の増大を一時的に抑え込んだとしても、感染者数が0人にならない限り(あるいは残った感染者を完全に封じ込めない限り)、対策を緩めると感染症にかかる人々は増大するようだ。
感染症に季節性がある場合
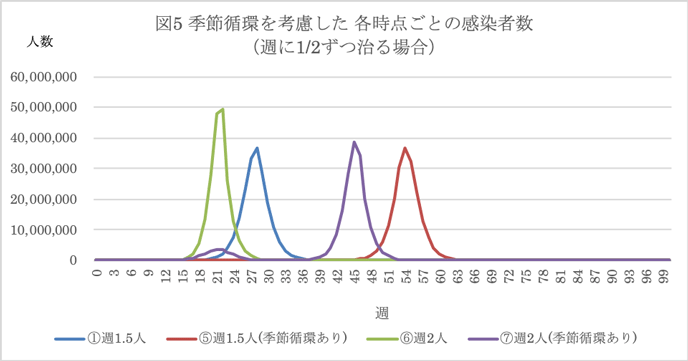
感染症に季節性がある場合(冬に多く夏至の頃にほとんど0になることを想定)のパターンも作ってみた。0週がおおむね1で26週でおおむね0となる正規分布の数値(以下では「季節常数」と呼ぶ)を作り、上記のbの代わりにb×季節常数を使って、後は同じように計算した。ただし、b=1.5の場合だけでなく分かりやすい例としてb=2の場合を含めた(図5)。
季節循環がある場合、図5では分かりにくいが、⑤週1.5人(季節循環あり)だと、21週の5.6万人をピークとして32週にいったん492人まで減少し、その後に再び増加を始めてピークは54週の3657万人になる。⑦週2人(季節循環あり)だと、21週で最初のピークが来て(347万人)、いったん収まってから次のピークが45週目に来る(感染者数は3869万人)。
終わりに
以上のシミュレーションは新型感染症についてのものではない。新型感染症について季節性も念頭に置いた緻密なモデルも作られているので、英語と数学のできる人はそちらを見ていただいた方が良い[2, 3]。
一般論として、重い感染症(死亡率が高かったり重大な後遺症が残るもの)については経済活動などを犠牲にしても強力な感染予防対策を長期にわたって講じて予防ワクチンや効果的な治療法ができるのを待つ方が良さそうだ。その一方で、軽い感染症であれば、感染しないと免疫ができないのであれば、経済活動への負担を考慮して、ある程度感染を許容するという選択肢もありそうだ。


