Economies experience a variety of local shocks: Natural disasters and weather related disruptions, discoveries of natural resources, disruptions of particular trade routes, corporate bankruptcies and other shocks to local firms, and labor strikes are a few examples. Moreover, industry shocks are local since industries are unevenly distributed in space. Many of these local shocks are too small to affect the aggregate economy and to have an impact that goes beyond the very town, firm, or industry that it affects directly. However, other shocks can have widespread effects on states, other sectors, and, importantly, the aggregate economy.
Japan experienced this first-hand with the economic effect of the earthquake and tsunami, as did cities like New Orleans in the case of Hurricane Katrina, or states like Michigan with the troubles of U.S. automakers, or California with inventions in the high-tech industry. Examples of local shocks abound, but do these shocks have sizable aggregate implications? Can we gauge and measure the effect of these shocks on aggregate outcomes? What does the elasticity of aggregate productivity, output, and employment depend on? Understanding the answer to these questions is essential for the design of policies to alleviate and manage the effect of shocks to the economy.
The potential importance of idiosyncratic shocks in generating aggregate fluctuations has long been recognized. Nevertheless, these types of shock were dismissed as an important source of aggregate fluctuations due to arguments based on the "law of large numbers". The idea is simply that the sum of these shocks averages out in the aggregate as we add a large number of 'small' shocks. This view has been recently challenged in a number of ways, both theoretically and empirically. For example, Gabaix (2011) argues that, if the units that receive the shocks are firms, these shocks will not average out unless the number of firms is unrealistically large. The reason is that the size distribution of firms is well approximated by a Pareto distribution and such a distribution, with its fat upper tail, implies that the law of large numbers converges very slowly; too slow for the number of firms in the U.S. to be large enough for idiosyncratic firm-level shocks not to matter. So the shocks to some of the large U.S. firms, like General Motors Company or Walmart, have a large impact on aggregate output.
Other research has focused on the effect of industry shocks on aggregate outcomes (see for example Acemoglu, et. al, 2012). This work has argued that even if productivity changes happen at the detailed industry level, these changes will not average out due to the structure of input-output linkages in the economy. In particular, the centrality of some sectors in the U.S. economy results in a skewed distribution of linkages between sectors, which leads some idiosyncratic shocks to have important aggregate consequences; a similar argument than the one for firms, but this time for industries and their forward and backward linkages. The oil industry is a good example of a central industry: one that a large number of other sectors use as a significant input.
The evidence on the importance of firm and industry shocks in generating aggregate fluctuations is convincing. However, it leaves aside an important dimension, namely, space. Not only are many of the idiosyncratic shocks spatial in nature, but firm and industry-specific shocks have an important spatial dimension. Shocks to a particular industry are likely to change the inputs sourced from this and other industries, as well as where these inputs are sourced from. This in turn will lead to different trade patterns across locations and distinct allocations of labor. That is, space matters not only because some of these shocks affect all producers locally, but also because some sectors and firms operate in particular locations. Economic activity is far from being uniformly distributed in space, and this is relevant for the propagation of idiosyncratic shocks. Namely, the elasticity of output or productivity to a productivity shock in a given sector will be a function of the distribution of that sector in space.
To understand these patterns, and eventually measure the importance of the different transmission networks, we need to specify first the key elements that characterize a location. In "The Impact of Regional and Sectoral Productivity Changes on the U.S. Economy," (with Caliendo, Parro and Sarte), we take a particular stand on this. We propose a model in which locations (which in the quantitative exercise will be represented by the 50 U.S. states) have different sectoral technologies, different stocks of immobile factors, and different geography (in terms of the bilateral transport cost between states by sector). Labor is assumed to move freely across locations.
With this specification in hand we can start thinking about the importance of space for the elasticity of aggregate economic activity to idiosyncratic shocks. A positive shock to a particular sector that is concentrated in certain states will increase production and productivity in those states, will attract some migration, and will redirect some regional trade towards these states as more states use their output as intermediate inputs. Productivity will grow as a result of the direct effect, but less proportionally due to the laxer firm selection. In other regions, productivity will tend to grow as a result of the shock, due to the tougher firm selection as producers relocate elsewhere and exit the state economy.
All of these effects are mediated by the geography of the economy. States that are relatively isolated will react differently to shocks than states that are centrally located as reflected in their bilateral trade costs. Isolated states are relatively bad providers of intermediate goods to other states and so their output will tend to expand less as a result of productivity shocks.
Consider further the role of migration and local factors. Local factors play a particularly important role in determining the elasticity of local and industry shocks. Some factors of production are undoubtedly fixed. The land of a state is essentially inelastic (although clearly some improvements that make some land more suitable for production or housing can be made). Other structures like highways, ports, stadiums, and concert halls can be built, but they are adjusted slowly over several years, if not decades. Other structures like houses and buildings are adjusted more frequently, and some other capital, like machines and equipment, are fairly flexible and mobile. Simple distinctions between mobile and immobile factors clearly leave some of these potentially important differences aside. Drawing this distinction amounts to deciding on the relevant time term of the analysis. In our paper we take the view that labor is mobile, equipment is traded every period as any other material input, and the rest of the structures are immobile. This amounts to a national share of immobile factors in the U.S. equal to 13% (as calculated by Greenwood, Hercowitz and Krussell, 1997). However, the share varies substantially by state. This is important. Consider a state with a very low stock of immobile factors per capita. If that state receives a positive productivity shock, the people that move in strain local resources. Immobile factors per capita are now even lower than before and the economy expands relatively little. The price of immobile factors increases, making everything in the state more expensive, and thereby decreasing the original migration flow. States with plenty of local factors will face the opposite effect. In the U.S., Illinois is such a state. Shocks that positively affect Illinois will therefore have a larger aggregate elasticity than shocks that hurt it.
The framework we propose can be quantified using a rich dataset that includes bilateral trade flows across states by sector, local income and factor use data, and a national input output matrix, among other variables. We then use the advances in the recent quantitative trade literature that permit solving large equilibrium trade models, and add the aforementioned local characteristics to go from an international to a regional trade framework. The result is a model that can be used to quantify the effect of local and sectoral shocks on aggregate and local outcomes. It can be readily applied to a variety of countries, although we have only used it for the U.S. at this point.
I will highlight some of the result we obtain using the particular example of a 10% productivity shock to the Computers and Electronics industry. The industry represents about 2.5% of the U.S. gross domestic product (GDP) in 2007 (the year of all of our calculations). The elasticity of aggregate output to a shock in this industry is 0.94. This is partly the result of the industry being fairly concentrated geographically in a state, California, with relatively abundant local factors. Compare this number with the 0.54 elasticity in construction which (being non-tradable) is one of the less concentrated sectors.
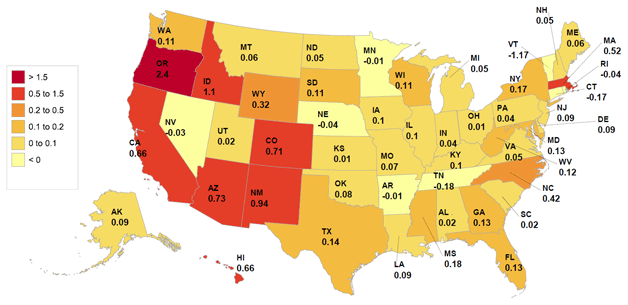
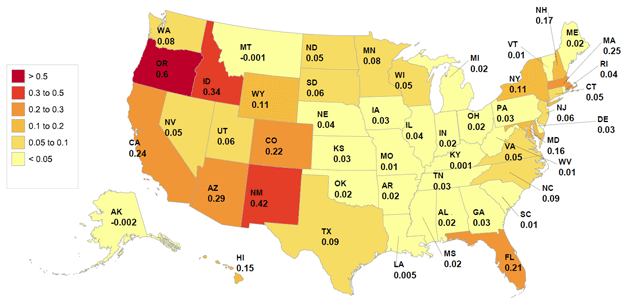
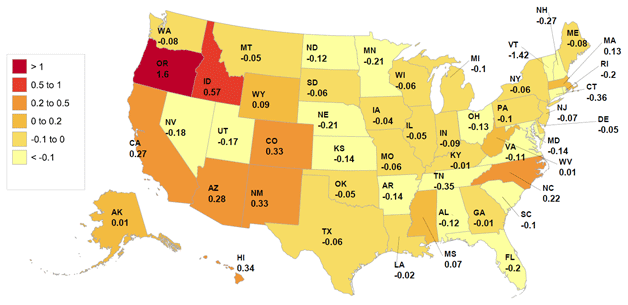
Figures 1 to 3 (copied from Figure 15 in our paper) represent the change in GDP, total factor productivity (TFP), and employment that our methodology predicts in all of the different U.S. states as a result of a 10% productivity shock to the Computer and Electronics industry. The impact across states is very heterogeneous. Some states like California and Massachusetts, that have traditionally been important producers in the industry, grow as a result of the shock. California's aggregate state GDP grows by 0.66%, its employment by 0.27%, and its measured TFP by 0.24%. The biggest winner from the shock to the Computers and Electronics industry is, however, Oregon, which benefits from its relatively important presence in the industry but also from its proximity to California and the state of Washington (the home of Microsoft Corporation), two important producers in the industry.
Of particular interest is that many of the states surrounding the two largest producers in the industry (California and Massachusetts) suffer negative consequences from the shock in terms of output and employment. Output goes down in Vermont, Connecticut, and Rhode Island, all of which are neighbors of Massachusetts. It also goes down in Nevada that neighbors California. The shock makes the states that are productive in the industry gain more, and attracts employment from other states. The states that decline are the neighboring states that do not use the industry as an important input in production.
In "The Impact of Regional and Sectoral Productivity Changes on the U.S. Economy," we do a variety of other counter-factual experiments. The interest of the different experiments probably depends on the actual shocks an economy has received recently. Regardless, in all of our experiments we find that, as in the case above, the spatial characteristics of the economy play a crucial role in mediating the shock. This underscores the importance of accounting for local factors and spatial interaction when analyzing aggregate fluctuations.
Hopefully, this type of quantitative exercise will be repeated for other countries in the future. Particularly interesting would be the case of Japan, which, as an island, is subject to its share of weather shocks, as was evidenced by the recent tsunami and the resulting disruptions. Such an exercise could assess the medium term impact of such an event on migration, productivity, employment and welfare. Furthermore, the concentration of the Japanese economy in sectors like Computers and Electronics make the above exercise particularly revealing. The exercise above suggests that the concentration of production in that industry in the U.S. led to a large elasticity of real GDP to industry shocks. Ultimately, the reliance of an economy depends on the magnitude of these elasticities. A word of caution is important: it is hard (or impossible) to extrapolate from one country to the other. Each country needs to do its due-diligence. The evaluation of policies to relocate production in space, disaster rebuilding efforts, or large federally funded infrastructure projects crucially depends on this analysis.


