| Author Name | Yingying DONG (University of California Irvine) / Ying-Ying LEE (University of California Irvine) / Michael GOU (PricewaterhouseCoopers) |
|---|---|
| Research Project | Economic Analysis of the Development of the Nursing Care Industry in China and Japan |
| Download / Links |
This Non Technical Summary does not constitute part of the above-captioned Discussion Paper but has been prepared for the purpose of providing a bold outline of the paper, based on findings from the analysis for the paper and focusing primarily on their implications for policy. For details of the analysis, read the captioned Discussion Paper. Views expressed in this Non Technical Summary are solely those of the individual author(s), and do not necessarily represent the views of the Research Institute of Economy, Trade and Industry (RIETI).
Macroeconomy and Low Birthrate/Aging Population (FY2016-FY2019)
Economic Analysis of the Development of the Nursing Care Industry in China and Japan
The regression discontinuity (RD) design is one of the leading quasi-experimental empirical strategies for policy evaluation. The standard RD design assumes a binary treatment. Many empirical applications of regression discontinuity (RD) designs, however, involve a continuous treatment. This is the first paper to provide identification and inference theory for RD designs with a continuous treatment. We utilize for identification any changes in the distribution of the continuous treatment at the RD threshold (including the usual mean change as a special case).
Consider our empirical question for concreteness. Are banks less likely to fail when they hold more capital? To provide a credible estimate of the causal effect of capital holdings on bank failure, we take advantage of the minimum capital requirements in the early 20th century of the United States.
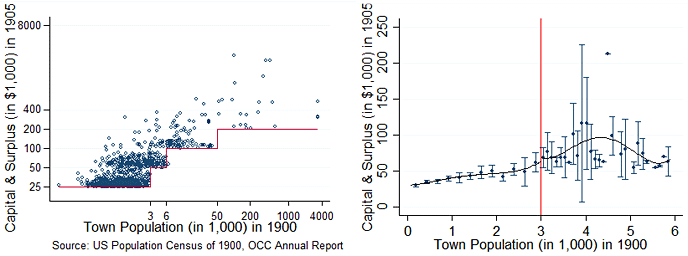
As shown in Figure 1 (left), the minimum capital requirements (marked by the solid line) is assigned based on town size – as town size crosses certain thresholds, minimum capital requirements jump up and hence the bottom of the capital distribution shifts up. Figure 1 (right) plots the mean capital against town size along with the 95% confidence intervals. No significant changes are found in the mean capital at the first policy threshold, where 80% of the banks are present. Estimating the causal impacts of capital holdings would be difficult by just applying the standard RD design, which requires that the average capital change at the policy threshold. However, taking advantage of lower quantile changes in the capital distribution allow for quantifying the causal impacts of increased bank capital.
We show that while the higher capital requirements induce small banks to hold more capital, these banks respond in a way to prevent the policy from having intended effects. In particular, a 1% increase in capital leads to a close to 1% increase in assets among all banks at the lower quantiles of the capital distribution. As a result, the long-run (up to 24 years, from 1905 to 1929) risk of suspension for those banks stays the same. These results help us better understand the frequent bank runs and banking panics prior to the Great Depression. These results are also useful in considering the current debate on the macroprudential vs. microprudential approach to financial regulation, where the later promotes higher capital requirements under the ratio regulation regime.
Our empirical example is not alone, many public policies or welfare programs do not necessarily target the average units. Instead they may target parts or features of the treatment distribution, such as changing the mean, changing the variance or shifting one or both tails of the distribution. Examples include minimum school leaving age, minimum wage, maximum welfare benefits, government transfers that are capped at certain levels, or pollution ceiling set by the environmental protection agency. By focusing on where the true changes are in the treatment distribution, our approach can provide what are likely to be the most policy relevant treatment effects.