| 執筆者 | 赤松 隆 (東北大学)/森 知也 (ファカルティフェロー)/高山 雄貴 (金沢大学) |
|---|---|
| 研究プロジェクト | 地域経済圏の形成とそのメカニズムに関する理論・実証研究 |
| ダウンロード/関連リンク |
このノンテクニカルサマリーは、分析結果を踏まえつつ、政策的含意を中心に大胆に記述したもので、DP・PDPの一部分ではありません。分析内容の詳細はDP・PDP本文をお読みください。また、ここに述べられている見解は執筆者個人の責任で発表するものであり、所属する組織および(独)経済産業研究所としての見解を示すものではありません。
地域経済プログラム (第三期:2011〜2015年度)
「地域経済圏の形成とそのメカニズムに関する理論・実証研究」プロジェクト
世界の都市化率は1950年30%から、2014年には54%に増加し(United Nations, 2015)、先進国に限れば値はより高く、西欧・米国・日本では、それぞれ、79%・81%・93%に及ぶ。OECD.statによれば、2011年時、日本のGDPの70%以上が都市圏、内30%は東京都市圏単独が占めている。
都市位置の決定には、地理的優位性など外生的要因が影響したとしても、同じ立地優位性を今日も保持する都市は少なく、現状の都市規模は、内生的な集積の経済による影響が大きいと考えられている。このような背景から、空間経済学では、適切な地域経済政策を導く上で、集積形成を内生的に説明できる理論モデルにより現実の集積分布を再現した上で、反実仮想実験により、与件の変化に伴う経済立地の変化、および、その厚生評価を行う研究が主流になった。しかし、多地域空間において複数集積が生まれるモデルは複雑系に属し、分析は注意を要する。本研究では、複雑系の系統的な理論分析を可能にする、円環多地域空間と離散フーリエ解析を用いた手法を提案するとともに、最近の文献におけるモデル選択の問題を指摘している。
一国経済における経済立地を分析するモデルの根本的な要件として、複数都市の形成を内生的に再現し得ることがある。一見自明なこの要件は、高い評価を受ける既存の研究成果においても必ずしも満たされていない。それは、空間経済学において一般的に採用されてきたモデル群が、厳密解析を容易にする目的で、2地域モデルを用いるなどして、地域間空間を極端に抽象化してきたことに起因している。近年、ミクロデータや詳細地理情報の利用が一般的になり、経済学では理論・実証を対として行う研究が主流になった。それに伴い空間経済学では、多地域モデルの採用が標準的になったが、多くの研究では、多地域空間におけるモデルの振る舞いの精査抜きで、現実データへの当てはめが行われている。
本研究では、「新しい経済地理学」において代表的な、Krugman (1991)とHelpman (1998)によるモデルを取り上げる。これらは、元々2地域モデルとして開発され分析されてきたが、後者は、Redding and Sturm (2008), Nakajima (2008), Michaels et al. (2013), Monte et al. (2015)などで多地域経済に拡張され、実証分析で広く用いられている。
これらのモデルでは、産業の輸送費に対する感度が立地パターンを決定づける。Krugmanモデルでは、輸送費感度が高い産業が2地域に対して均等に分散し、低い産業は1地域に集積する。一方で、Helpmanモデルでは、逆の集積・分散パターンとなる。Krugmanモデルにおける分散は2地域に分散した市場への輸送費が、Helpmanモデルでの分散は地域内の通勤費用や混雑が原因となるが、集積・分散は、いずれのモデルにおいても全く同様に表現される。
本論文では、主要な結果として、これら2つのモデルで表現される集積と分散の形態が、多地域経済においては図1で示されるように質的に大きく異なることを示している。より具体的には、Krugmanモデルにおける分散は、小規模の集積が広範囲に分布する「局所的集積・大域的分散」の形態をとる一方、Helpmanモデルでは、高々単峰の人口・産業立地分布が実現するのみで、集積が起こる場合は常に一極集中的、分散はその集積の尖度の低下を意味する。Krugmanモデルとの対比で表現すれば「大域的集積・局所的分散」の形態をとる。
Helpmanモデルを複数都市経済に当てはめるRedding and Sturm (2008)以降の一連の実証分析では、モデルと現実データの乖離は「観察されない都市固定アメニティ」として解釈され、一見、モデルは現実経済を十分に再現しているかのように見える。しかし、実際には、都市規模の変動の殆どは、「観察されない都市固定効果」、つまり、モデルで説明されない「残差」に吸収されている。

たとえば、Redding and Sturm (2008)では、1939年のドイツの都市規模分布に対してモデルカリブレーションを行っているが、実際の都市規模の変動の約90%は、残差である。図2は各都市の「観察されない都市アメニティ」(AMENITY)に対して都市規模(SIZE)をプロットしたものである。
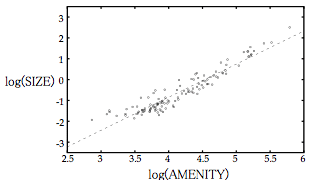
点線は以下の回帰におけるモデル推定値を示している (括弧内は標準誤差)。
実際には、これらの論文では、単峰集積すら起こらない「完全分散」の下でカリブレーションは行われている。つまり、集積を内生的に再現し得る設定ですらなく、集積が起こる要因は、地理的中心性など、立地空間の非対称性のみとなる。いずれの論文でも、一意均衡であることを利用してカリブレーションが行われるが、そもそも、内生的な集積が起こるモデルにおいて、均衡が一意である場合は、一極集中や完全分散など、極端な立地パターンが起こる場合であり、現実的に意味のある状況であることは少ない。
集積形成と関連する最近の話題としては、地域創生や、北陸新幹線や北海道新幹線の開業の経済効果などがある。当該地域における既存集積の変化や、新たな集積形成の可能性が分析の対象となるが、意味のある分析を行うには、第1に、複数集積を説明し得るモデルを採用する必要があり、その是非は、モデルの2地域経済における振る舞いからは判断出来ない。本論文では、集積の動向が鍵となるこのような政策評価において、適切なモデル選択を行うための系統的な解析ツールを提案している。
- 文献
-
- Helpman, E. 1998. "The size of regions." In Topics in Public Economics: Theoretical and Applied Analysis. eds., by D. Pines, E. Sadka and I. Zilcha: Cambridge University Press: 33-54.
- Krugman, P. 1991. "Increasing returns and economic geography." Journal of Political Economy 99(3): 483-499.
- Nakajia, K. 2008. "Economic division and spatial relocation: The case of postwar Japan." Journal of the Japanese and Internation al Economies 22(3): 383-400.
- Michaels, G., Rauch, F. and S.J. Redding. 2013. "Task specialization in U.S. cities from 1880-2000." Unpublished.
- Monte, F., Redding, S.J. and E. Rossi-Hansberg. 2015 "Commuting, migration and local employment elasticities." Unpublished.
- Redding, S. and D. Sturm. 2008. "The costs of remoteness: Evidence from German division and reunification." American Economic Review 98(5): 1766-1797.

