| Author Name | Adrien BLANCHET (Université de Toulouse) / Pascal MOSSAY (University of Reading and CORE) / Filippo SANTAMBROGIO (Université Paris Sud) |
|---|---|
| Research Project | Theory and Empirics of Urban Growth and Spatial Structure |
| Download / Links |
This Non Technical Summary does not constitute part of the above-captioned Discussion Paper but has been prepared for the purpose of providing a bold outline of the paper, based on findings from the analysis for the paper and focusing primarily on their implications for policy. For details of the analysis, read the captioned Discussion Paper. Views expressed in this Non Technical Summary are solely those of the individual author(s), and do not necessarily represent the views of the Research Institute of Economy, Trade and Industry (RIETI).
Regional Economies Program (FY2011-FY2015)
Theory and Empirics of Urban Growth and Spatial Structure Project
The agglomeration of households and firms in urban centres is an active field of research. Most works in the existing literature focus on the study of agglomeration forces mediated by the market mechanism. For instance, New Economic Geography (NEG) models stress the importance of increasing returns to scale in explaining the spatial concentration of economic activities.
In this paper, we address the role of non-market forces in contributing to the agglomeration of individuals in cities. In particular, we study how social interactions between individuals can shape the distribution of urban centres. The model builds on a framework due to Beckmann (1976), revisited by Fujita and Thisse (2002), and more recently by Mossay and Picard (2011). In these previous works, the internal distribution of the city was solved for a one-dimensional economy with agents having very specific preferences of land consumption.
In this paper, we look at whether the qualitative properties of the model still hold in more general environments. To this aim, we consider a two-dimensional spatial economy with individuals having general preferences regarding land consumption. We provide some conditions under which the spatial economy admits an equilibrium, and under which this equilibrium is unique.
So as to illustrate the scope of our results, we present several examples including two-dimensional spatial economies, coastal cities, and urban amenities.
Examples of a two-dimensional coastal city and of multiple agglomerations along a circular economy
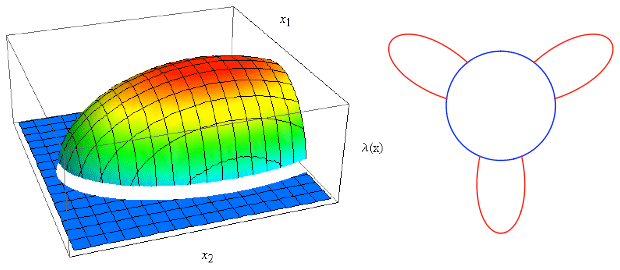
Our work generalises Beckmann's framework to the case of two-dimensional spatial economies with individuals having a concave increasing utility of land. Interestingly, it shows that spatial equilibria can be derived as minimizers of some functional. This is a useful result because these minimizers are in general easier to study and to determine than spatial equilibria themselves. In our model, the emergence of multiple of equilibria is due to a lack of convexity. While, along a line segment, a single agglomeration emerges, multiple ones emerge along a circular economy. Here, the origin of multiple equilibria is different from that in the urban model of Fujita and Ogawa (1982) which is driven by agglomeration forces mediated by the market.
The policy implications which can be drawn from our work are the following ones. First, non-market forces and urban amenities along with market forces should be considered as factors explaining the emergence and the internal distribution of spatial agglomerations. Second, by isolating the conditions under which a unique urban pattern arises, our work highlights the pervasive nature of multiple equilibria in spatial economics. So, in this context, the evolution of urban patterns is subject to history as transitions from one equilibrium to another are possible. Moreover, policy makers may be interested in designing policies which guide the transition to some preferred outcome.

